【Think!Think!】ちかみちレース

思考センス育成教材 Think!Think!（シンクシンク）のゲーム毎のプレイ方法やコツを紹介しています。

今回はスタンダードコースでプレイできる　ちかみちレース（近道レース）　です。

問題の概要

ゲームの内容は、画面の中に直線で結ばれた場所が何点か表示されます。

（下の画面例ではスタート・ゴール含め、９箇所）

そして、スタートからゴールまでの移動が最短経路になるようなポイントを選択するもの。

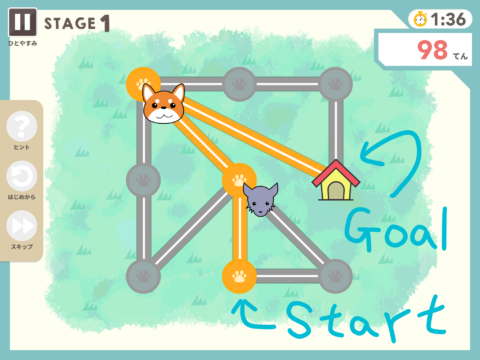
２匹の犬が別の経路で移動するので自分が選んだ道を通る犬が勝てば成功です。

犬は同じ速さで進むので、単純に距離だけの問題となります。

攻略のポイント

成功のコツとしては、斜めの移動ですかね。

中学生で三平方（ピタゴラス）の定理のあたりで習う気もしますが、直角三角形は斜辺の方が、それ以外の２辺の長さの和より短くなることがわかっていますのでコレを利用します。

あとは、今いる地点でゴールから離れる方向には進まないで良いです。

（上の画面例では他に選択できないのでいったん遠ざかっていますが。）

わざわざピタゴラスを使って説明しなくても、直感を信じて選べば良い気もしますね。

ポイントまとめ

• できるだけ、ゴールから遠ざからないように動く
• 斜めが使える場合は斜めに移動する

問題のレベルが上がって、複雑になってもこのポイントで大丈夫、なはず！

もし曲がりくねった道などが出てきたら分かりませんが、直線の距離だけ考えましょう。

コラム

２つの地点を結ぶ距離の考え方って実はいくつかあるんです。

• ユークリッド距離（一般的な距離）
• マンハッタン距離（市街地距離）
• チェビシェフ距離（チェス盤の距離）

三平方の定理的な計算で得られるのは、ユークリッド距離ですね。

マンハッタン距離は碁盤の目のような道をたどる時の距離です。斜めがありません。

マンハッタンの市街地がこのようになっているそうですが、日本だと京都の市街地をご存知の方はそっちの方がイメージ湧きますね。

チェビシェフ距離はチェスのように、縦も横も斜めも１マスとして数えます。

比べると、こうですかね（誤解していたら申し訳ないです）

チェビシェフ距離≦ユークリッド距離≦マンハッタン距離

他にも、プログラマ的にはハミング距離があったり、機械学習の分野ではマハラビノス距離なんかがあったりします。

世の中にもたくさん利用されていて、やはり距離って大事な概念です。

ちかみちレースでは、ユークリッド距離の積み重ねで最短経路を見つける練習をします。

Think!Think!で慣れておくと、中学・高校での数学も取っつきやすくなる気がしますね。

勉強の王道はコツコツと練習して、実際にできるようになることだと思います。

それがゴールへの近道だと思います。

以上、ちかみちレース（と一般的な距離）の紹介でした。

Think!Think!アプリは、こちらからダウンロードできます！

関連記事＞＞＞Think!Think!紹介記事・ゲーム一覧・イベント一覧・まとめページ